曲線，一個更接近完美的答案

編注：視頻文字稿內容由少數派整理以方便閱讀查找，要了解完整信息，建議直接觀看視頻。

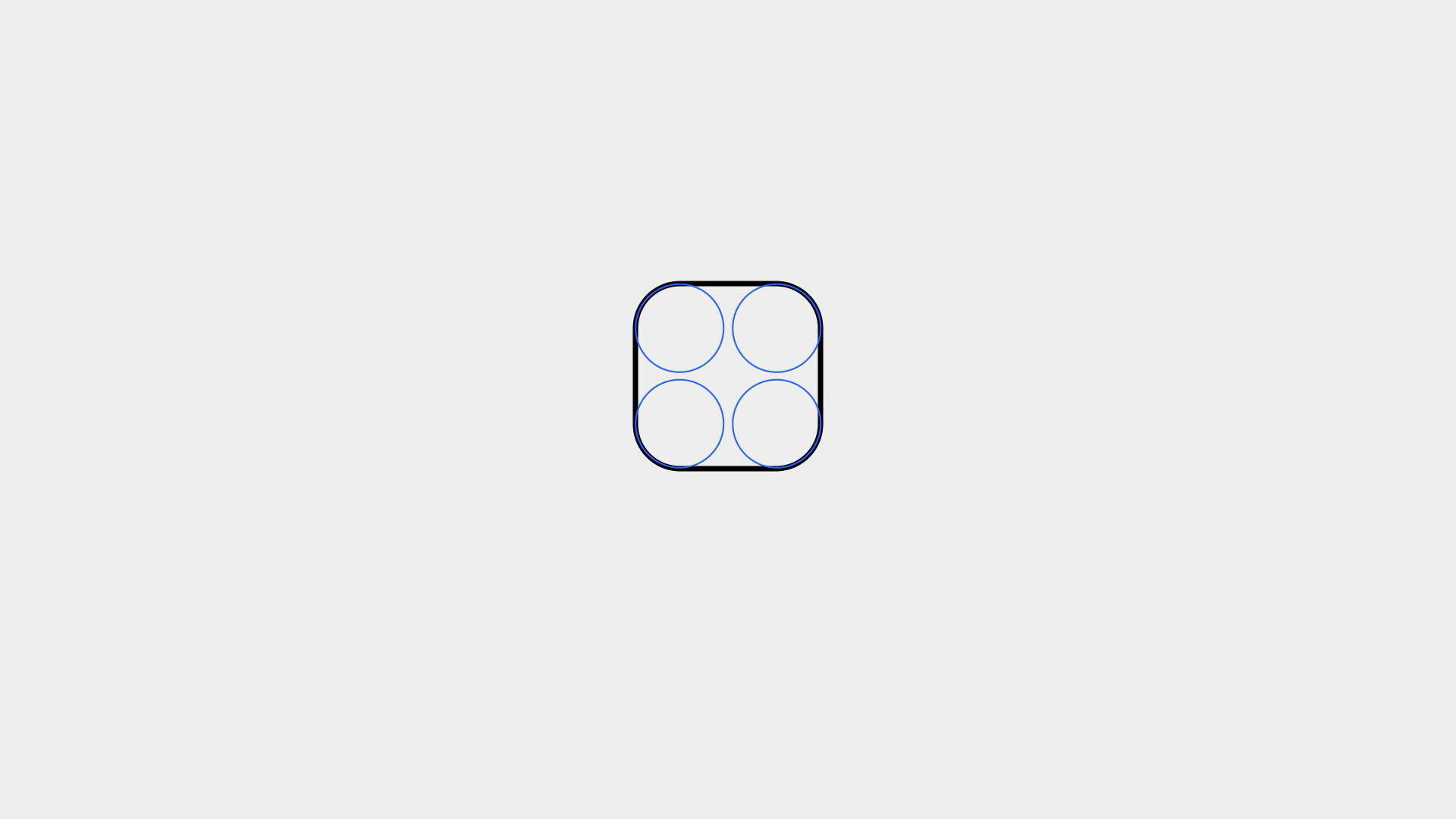
這是一個完美的正方形，每條邊都十分平滑、順暢，沒有瑕疵。試著把尖角變成 1/4 的圓進行連接，便得到了一個圓角矩形。在大多數平面繪圖軟件中，圓角矩形都是用這種方法繪制出來的。但是它的線條足夠順滑嗎？

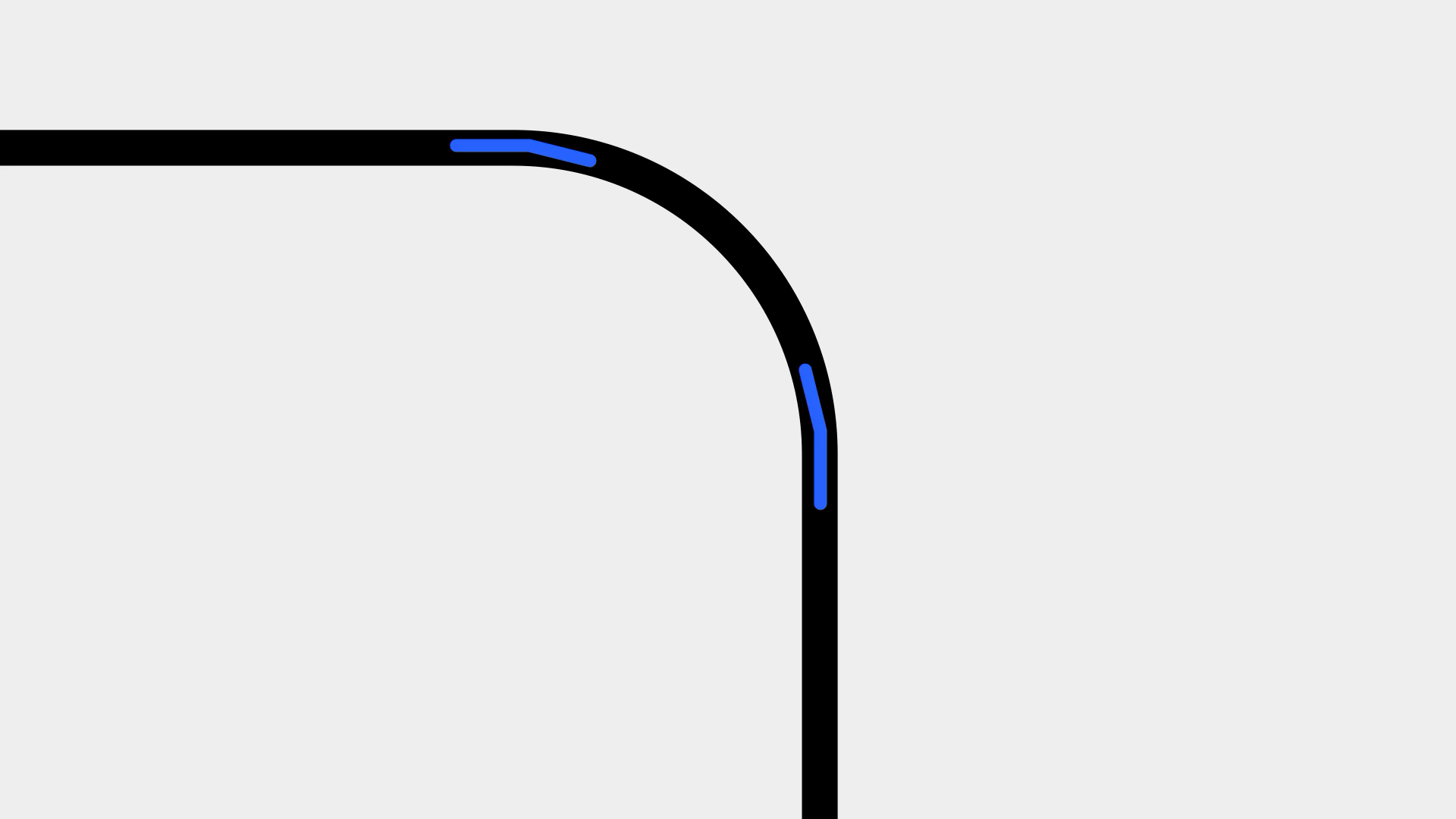
我們放大它的一角，在曲線與直線連接的地方過渡其實是不自然的。200多年前，人們便開始嘗試對平滑過渡的曲線進行計算，于是后來便誕生了很多種緩和曲線，在諸如測繪、工業設計之類的工作中起著十分重要的作用。

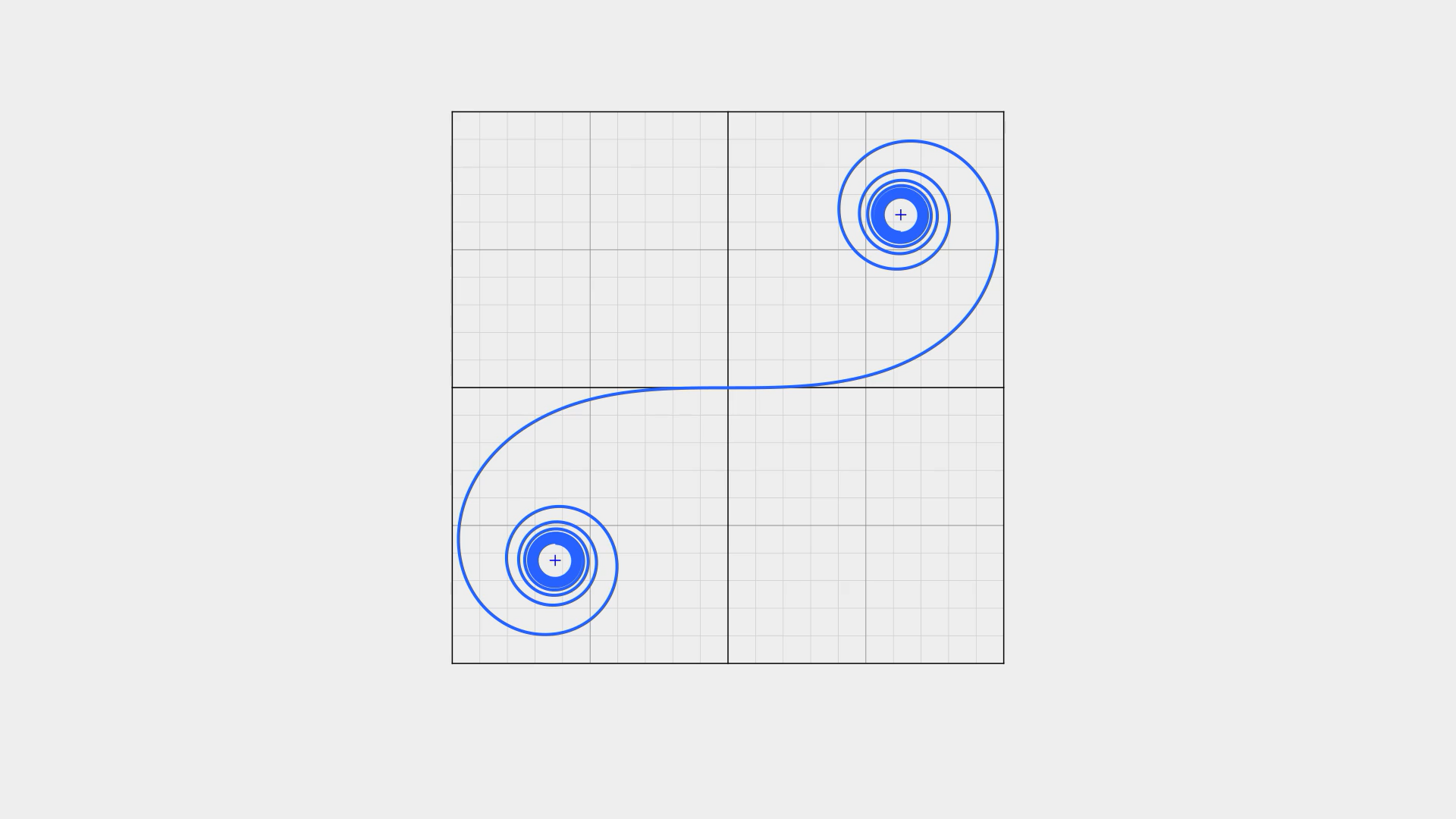
畫面中的「羊角螺線」就是其中之一，我們使用羊角螺線起點處的這段曲線繪制一個圓角矩形，會得到一個過渡十分順滑的結果。相比之下，右邊那個簡單粗暴的圓角矩形，也就顯得十分粗糙。

而經過優化的形狀，與 中 App 圖標的輪廓看起來幾乎一模一樣。在 iOS 7 之后，蘋果開始大規模采用這種曲線過渡的規范，使得「曲率連續」這個概念不再由專業設計師獨享，而是成為了更多愛好者們所熱衷的話題，「G2 連續」這個詞也被更多人所熟知。

僅僅是點與點的貼合可以稱為「G0 連續」，在點與點連續的基礎上如果還有相切關系，那就可以稱為「G1 連續」，而如果它們的曲率還有著更為連續的變化，可以稱為「G2 連續」。當然，這種描述并不精確，但是理解至此暫且足夠。

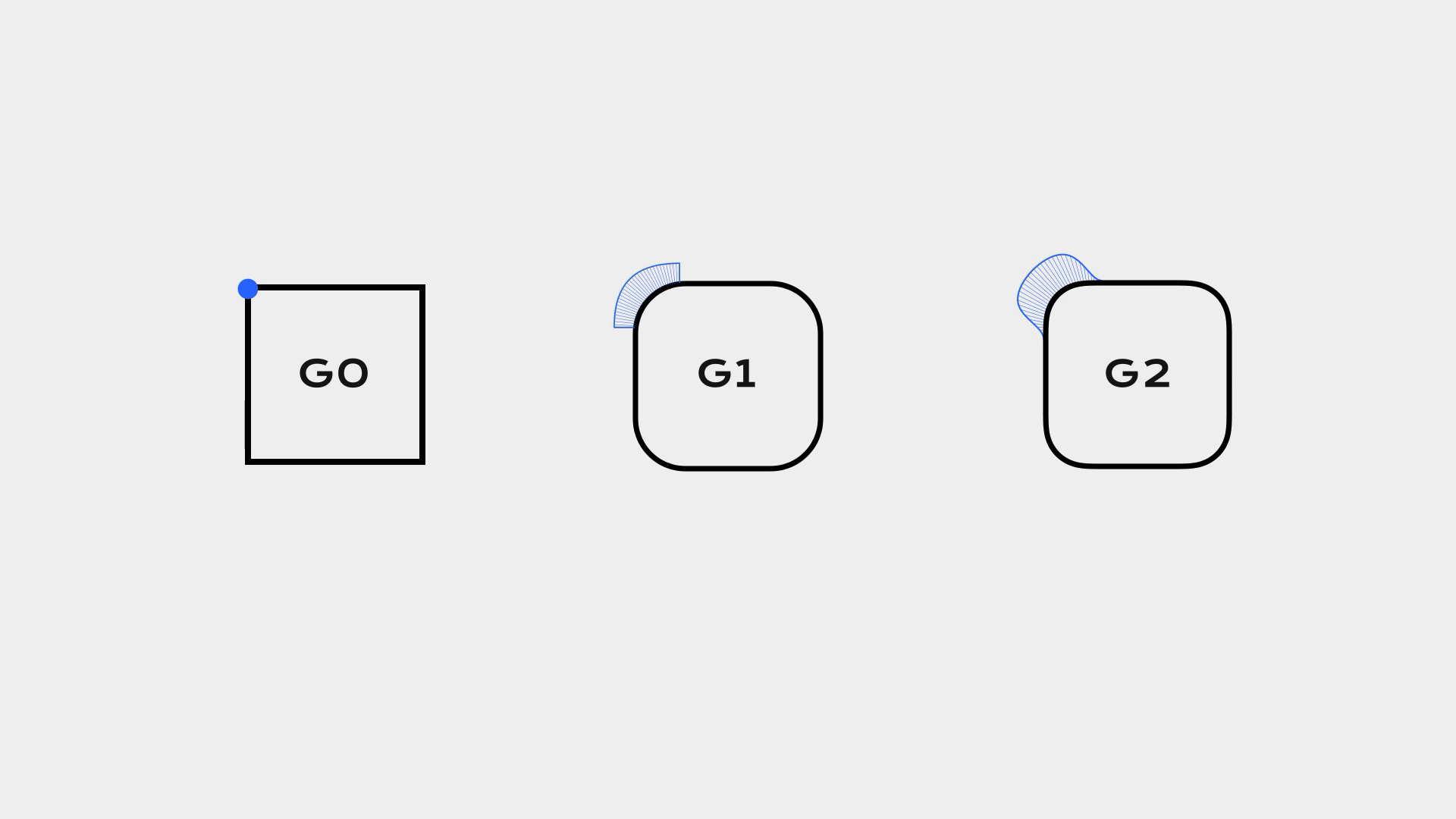
用通俗點的方法來說，其實就是讓曲率以一種看起來好像先慢后快的方式達到峰值，使其更加順滑，這與動畫中的速度曲線倒還有那么一點點的異曲同工之妙。如果以勻速前進，看起來就會比較生硬，而如果讓它突然加速再緩慢停止，就會模擬慣性，產生一種絲滑的感覺。

在很多平面軟件中繪制曲線的功能被稱為「鋼筆工具」，而它們的本質一般都是一種叫做的「貝濟埃」的曲線，其實更多時候人們愿意稱其為「貝塞爾」。這次所聊的 Bézier 曲線由法國人提出，所以按照法語發音應該叫做「貝濟埃」更為恰當。

這是一種通過設定幾個點然后插值進行擬合的方法，數理邏輯在這里不做深究。我寫了一個模擬程序進行演示，看看就好。

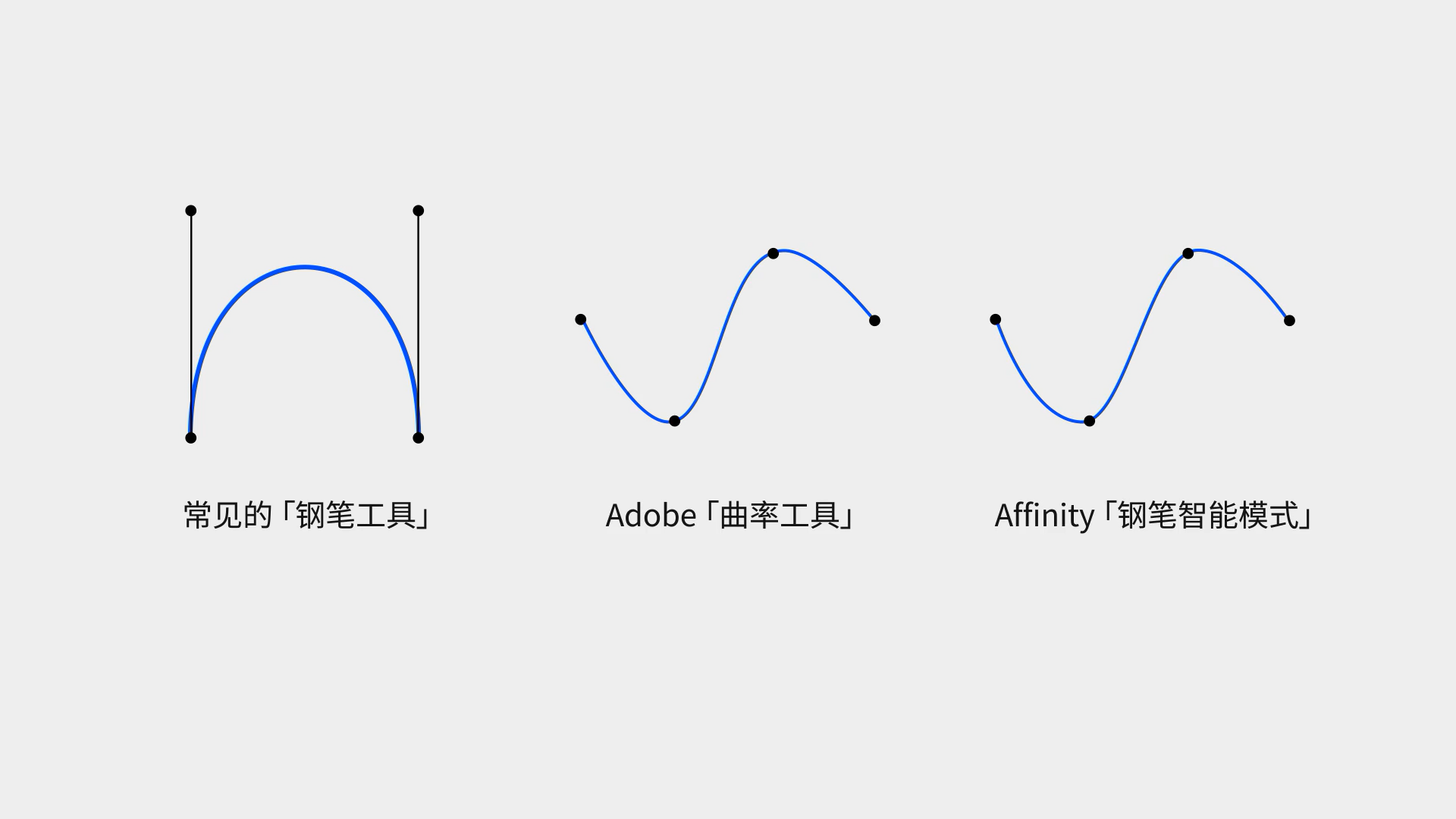
通過遞歸的方式，我們可以繪制出更高階的貝濟埃曲線。以 、 為首的平面軟件產品，采用的都是三次貝濟埃曲線。但 的曲率工具和 的鋼筆智能模式分別使用了完全不同的算法，這兩種算法產生的曲線必然經過節點，無法通過手柄進行靈活的調整，但是卻能夠自動生成較為順滑的曲線，在 CAD 中這比較常見，這里就不多贅述了。

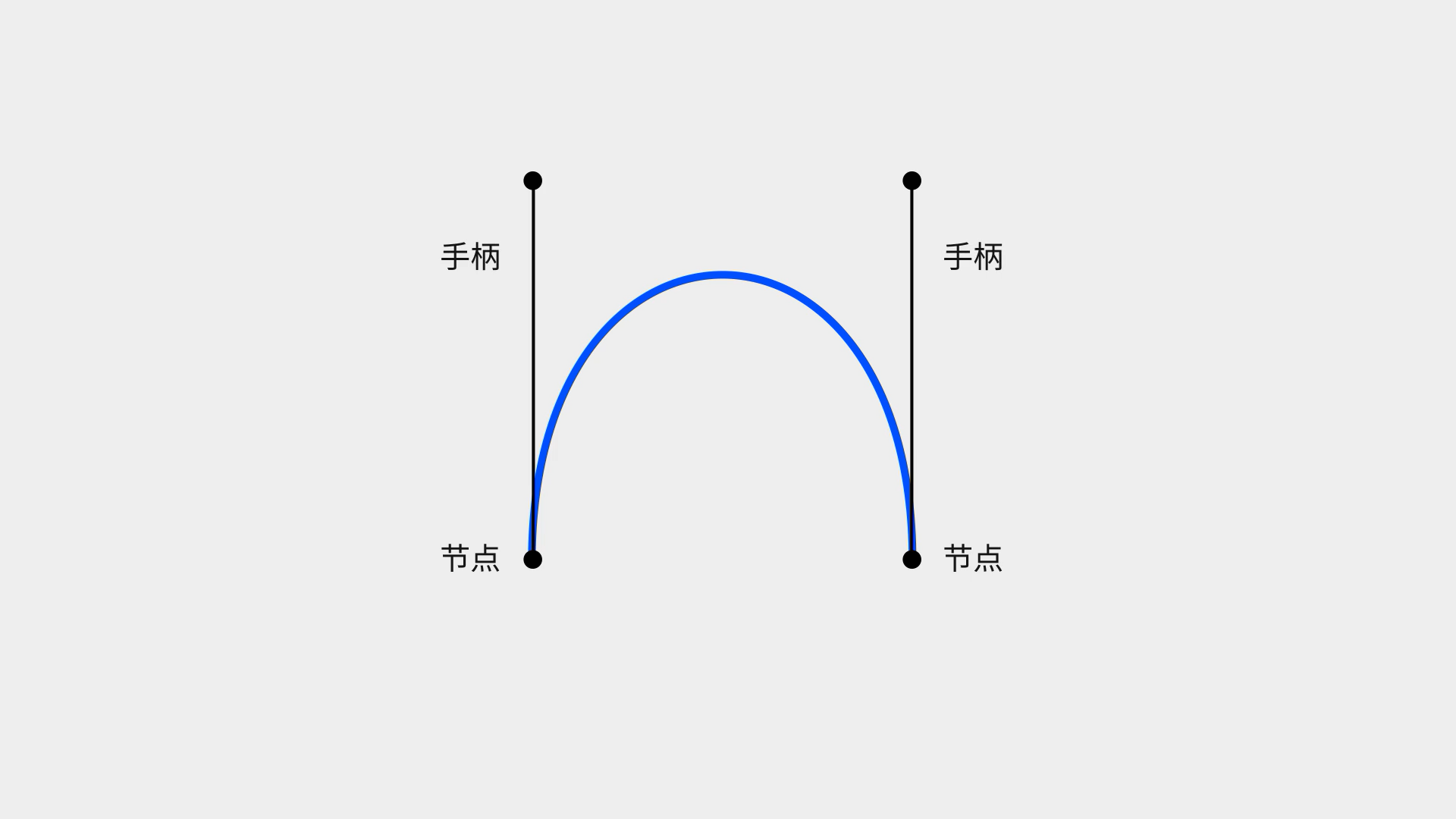
去掉三次貝濟埃曲線內部的杠桿，便是我們所熟知的鋼筆工具的模樣了。起始點與結束點就是我們在軟件中繪制的節點，而其余兩個點形成了我們用來調整曲線的手柄。設計師們如何才能在節點繁多、復雜的情況下，繪制出連接更順滑的曲線呢？

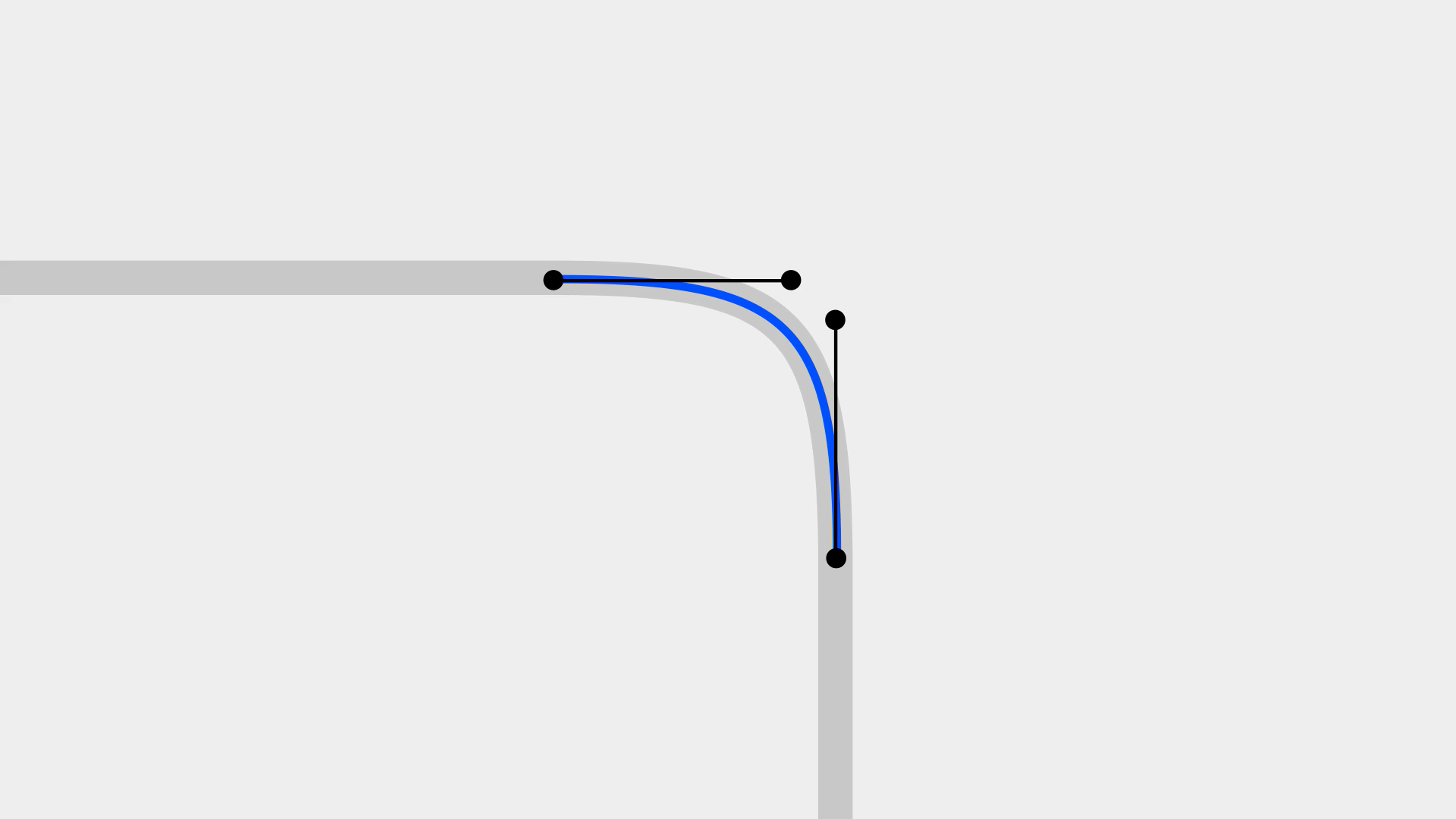
回到短片開頭，那個粗糙的圓角矩形，我們將每一個節點向內進行偏移，然后再適當拉長手柄，其實就可以對曲率連續進行一定程度的優化。這種調整在數理上并不精準，但在平常的工作中如果只是為了滿足觀眾的視覺其實已經足夠了。

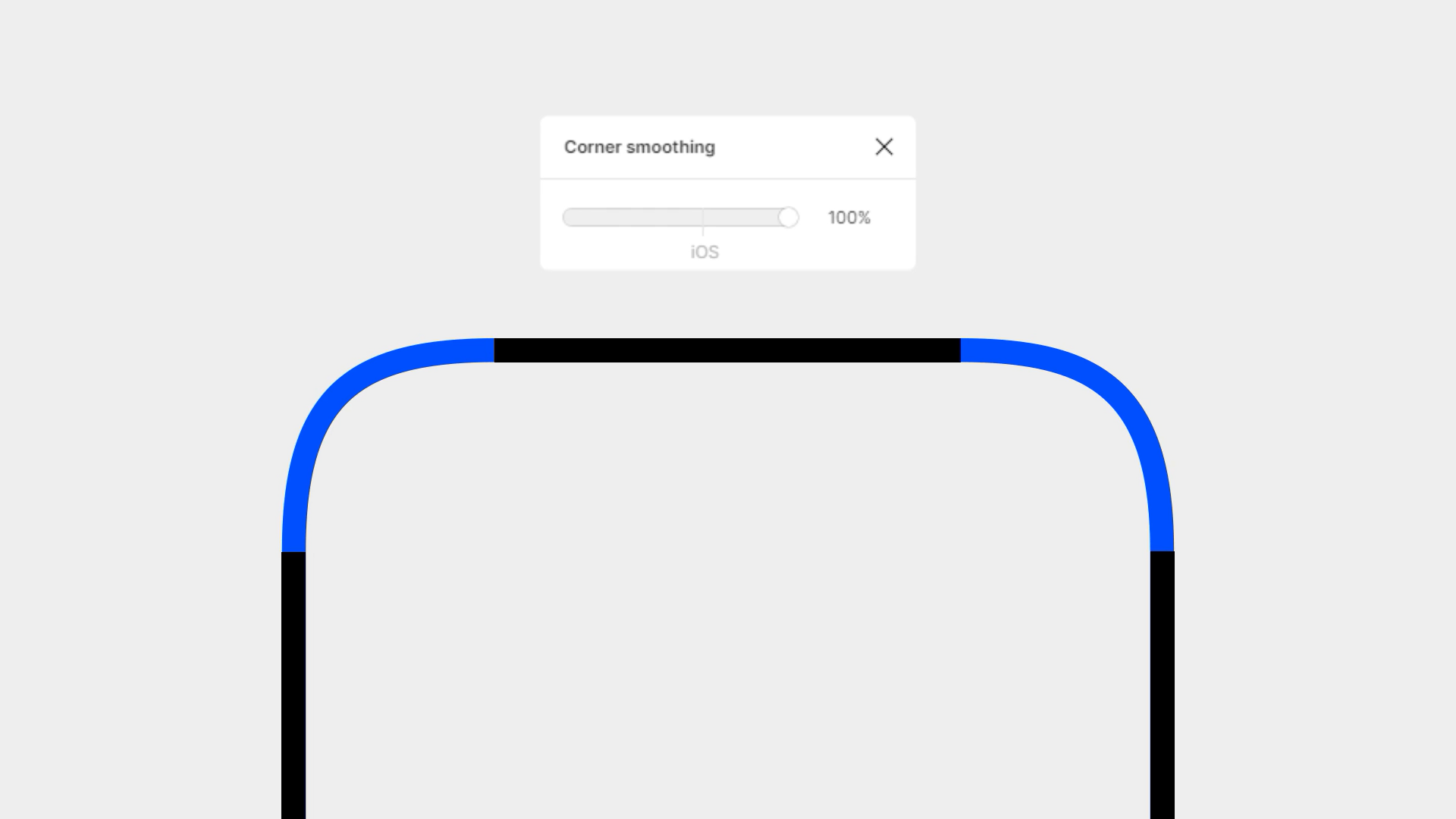
有一些軟件中有著相關功能，比如 中的 原生就能滿足這個需求。

在使用貝濟埃曲線進行繪制的時候，有著一個重要的規范。首先要盡可能的將節點放在「極值點」的位置，然后讓節點與手柄保持水平或垂直對齊，這可以讓繪制變得更加容易。因為這樣只需要調整手柄的長度就可以擬合自己想要的曲線結果，這個規則在字體設計中尤為重要。

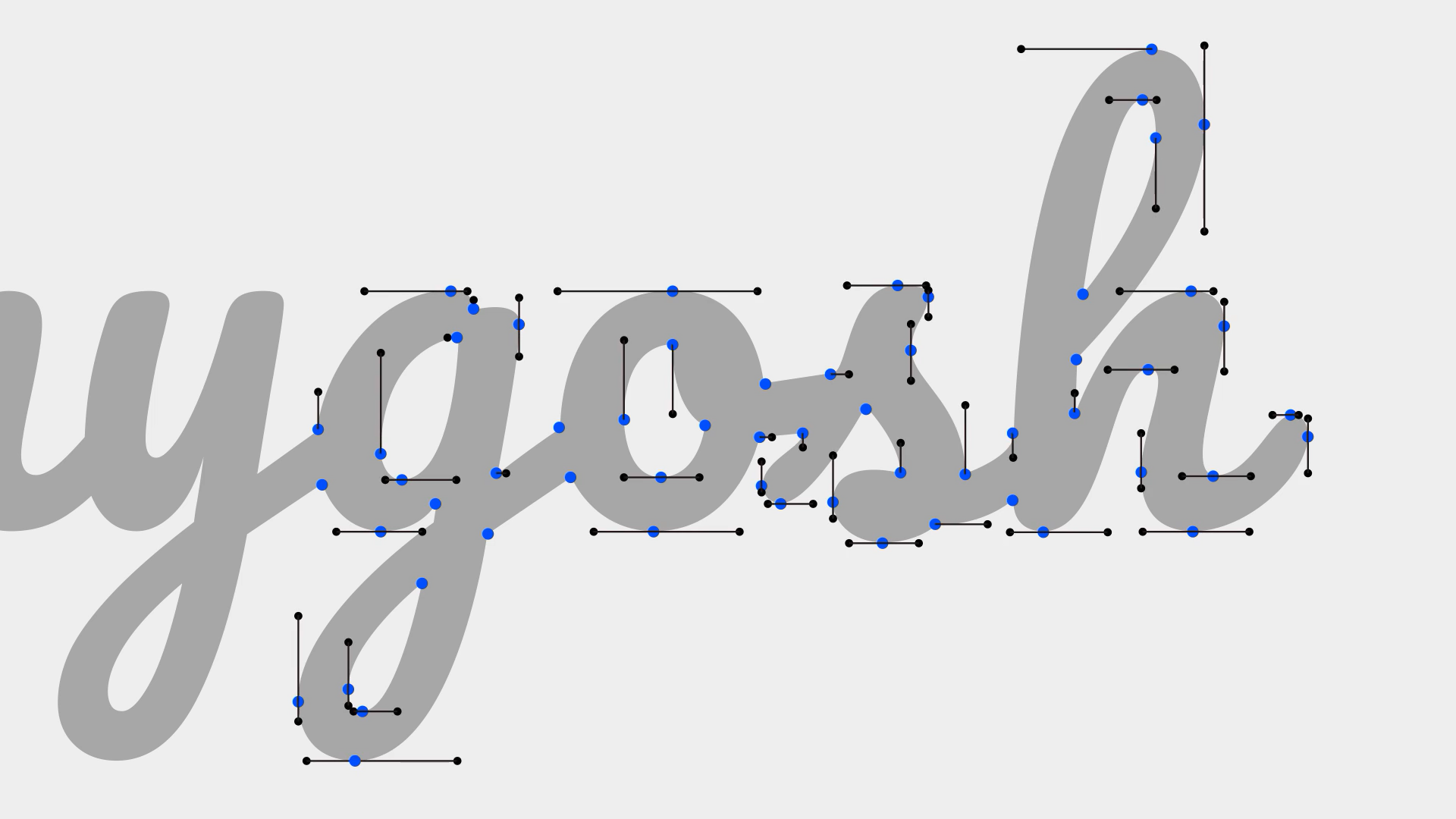
因為在低精度屏幕上，算法會根據這種位置的節點對顯示效果加以優化，專業的字體設計軟件甚至會有自動添加極值點的功能，但是在例如宣傳美術、藝術插畫領域等，這些最終會輸出固定精度位圖的情況，倒也可以適當放松標準。

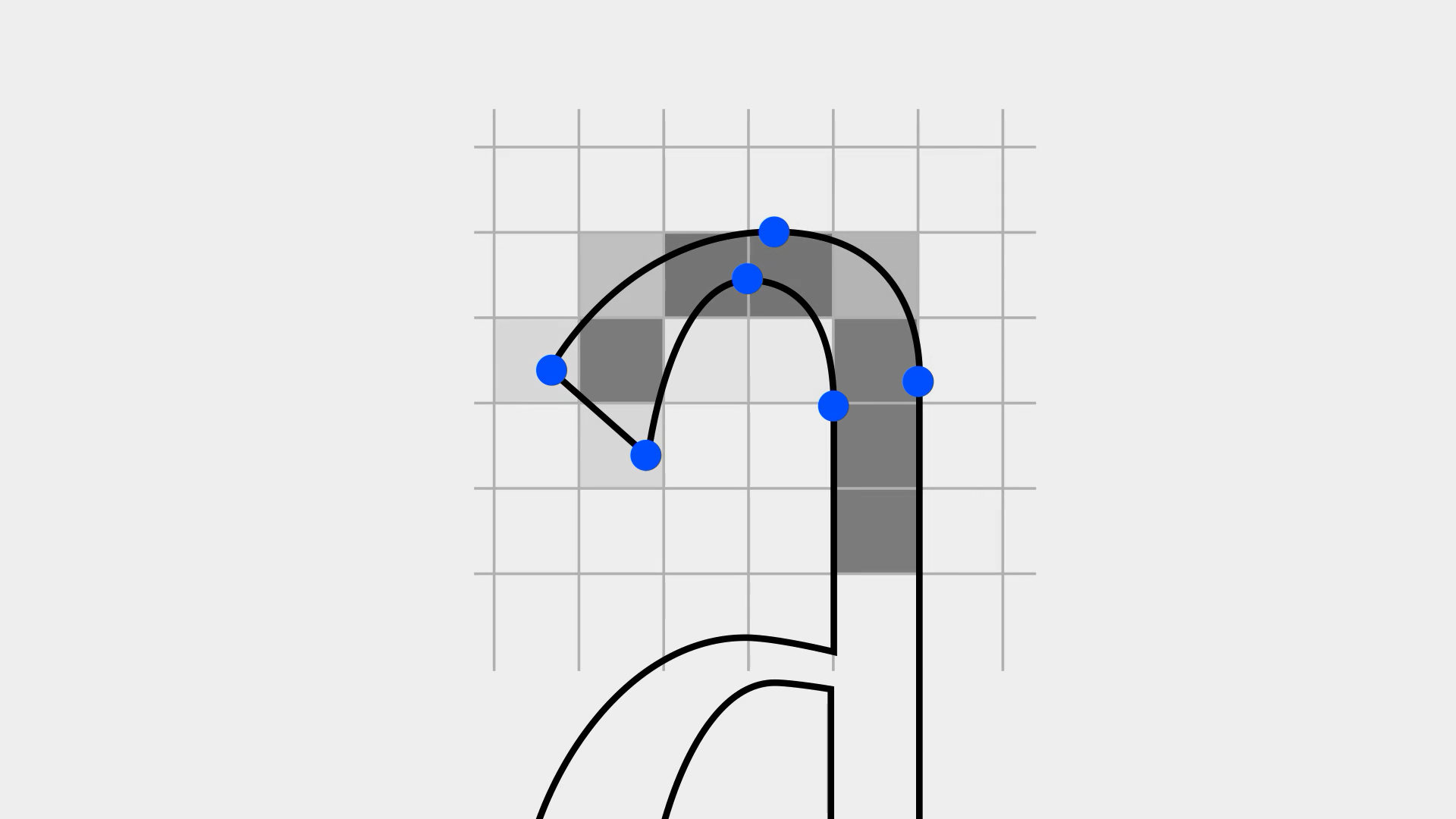
在字體設計領域中也有著經典的案例，「筑紫明朝體」是一款應用于印刷及平面設計領域的字體，并不是為了在數位屏幕上顯示而設計的。藤田重信用極少的節點數量繪制了優美的曲線線條，相應地也就降低了字體文件的大小，品質極高。

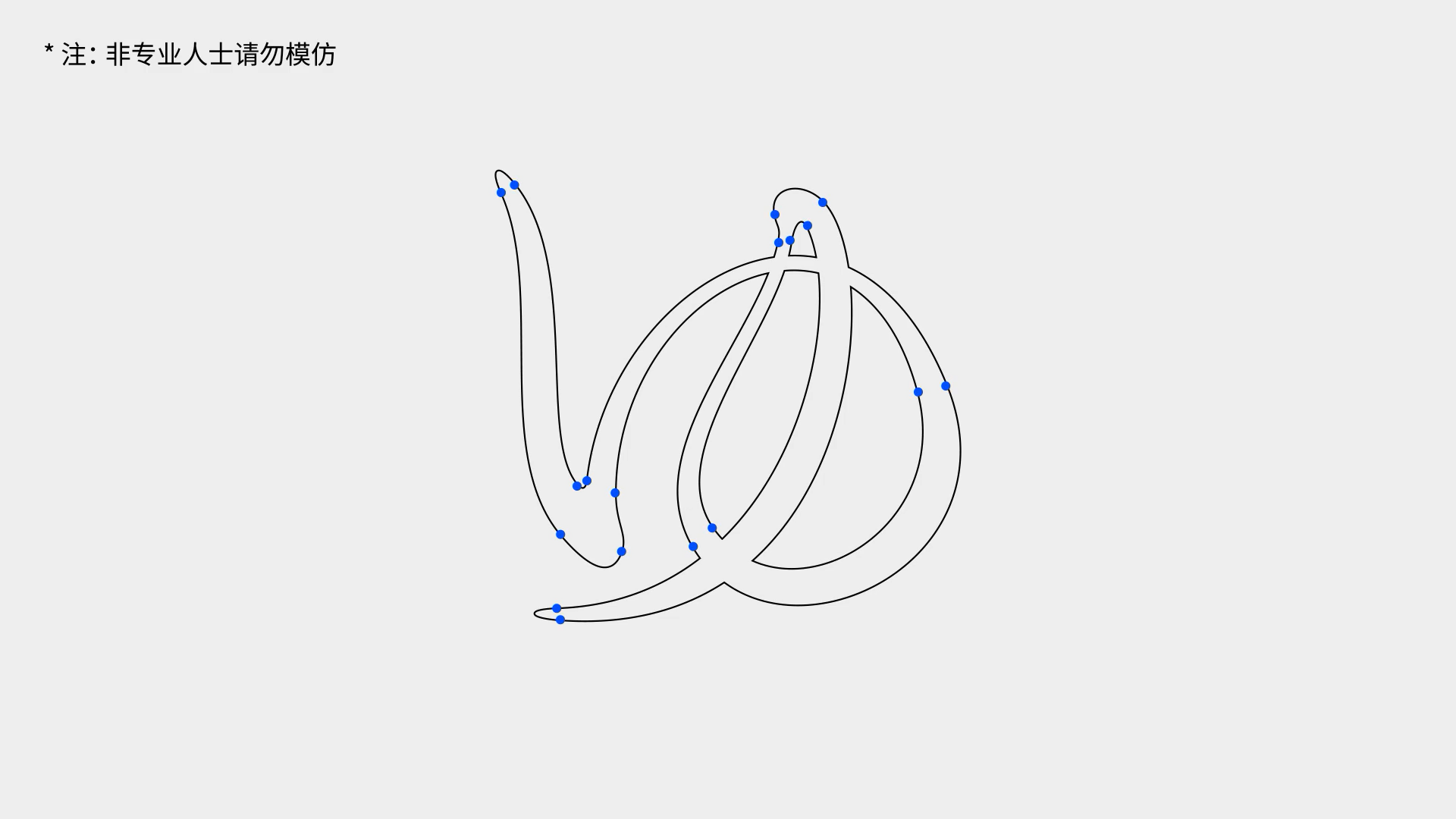
了解了這些規范，我們嘗試著繪制這樣的一個形狀。你可能會在起始、結束、中間設定三個節點構成這個形狀，但這樣我們會發現線條中間出現了不順暢的情況，還需要對這個節點進行單獨的調節。而調整后，他與手柄也無法以水平的對齊方式存在了。

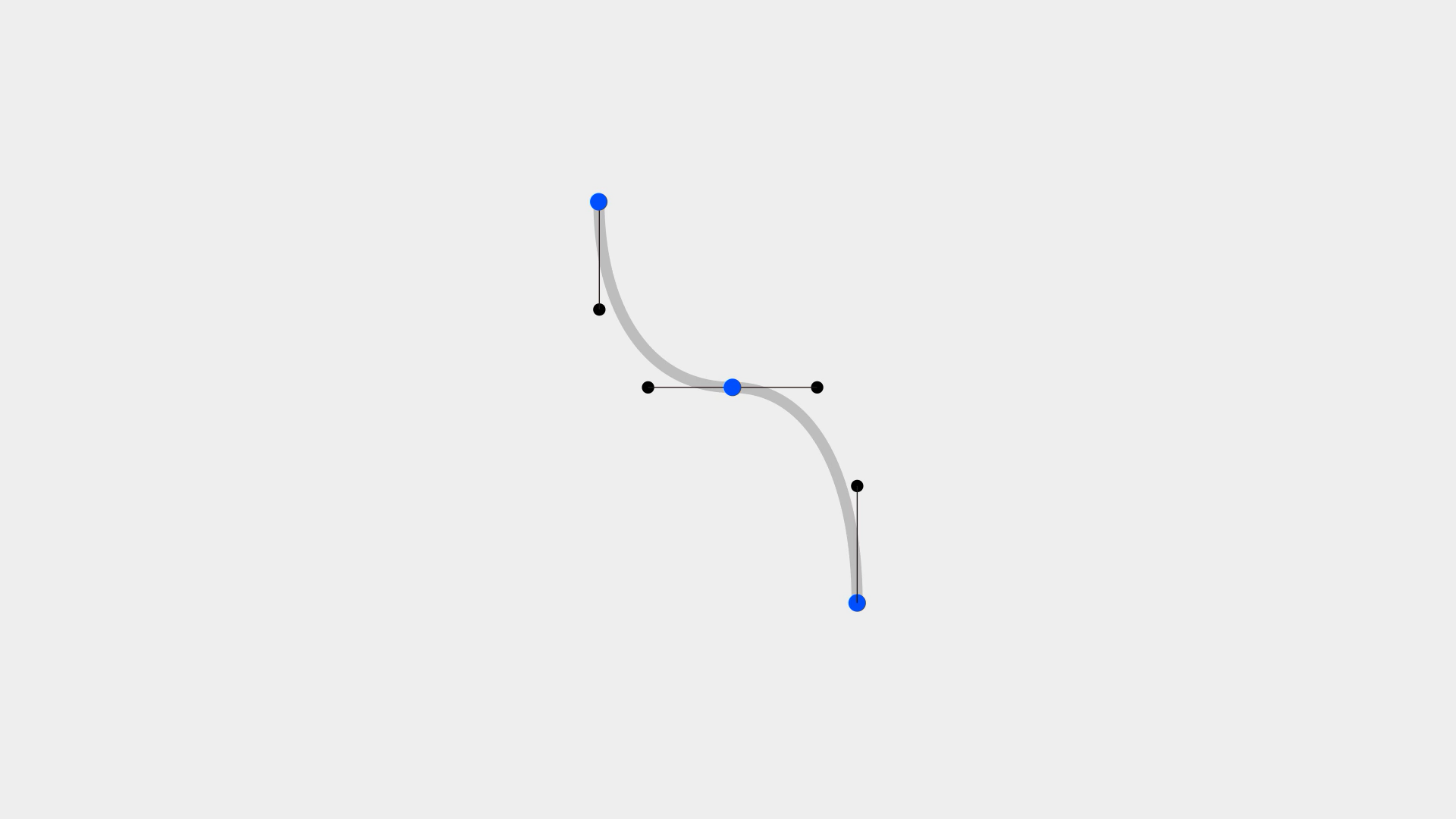
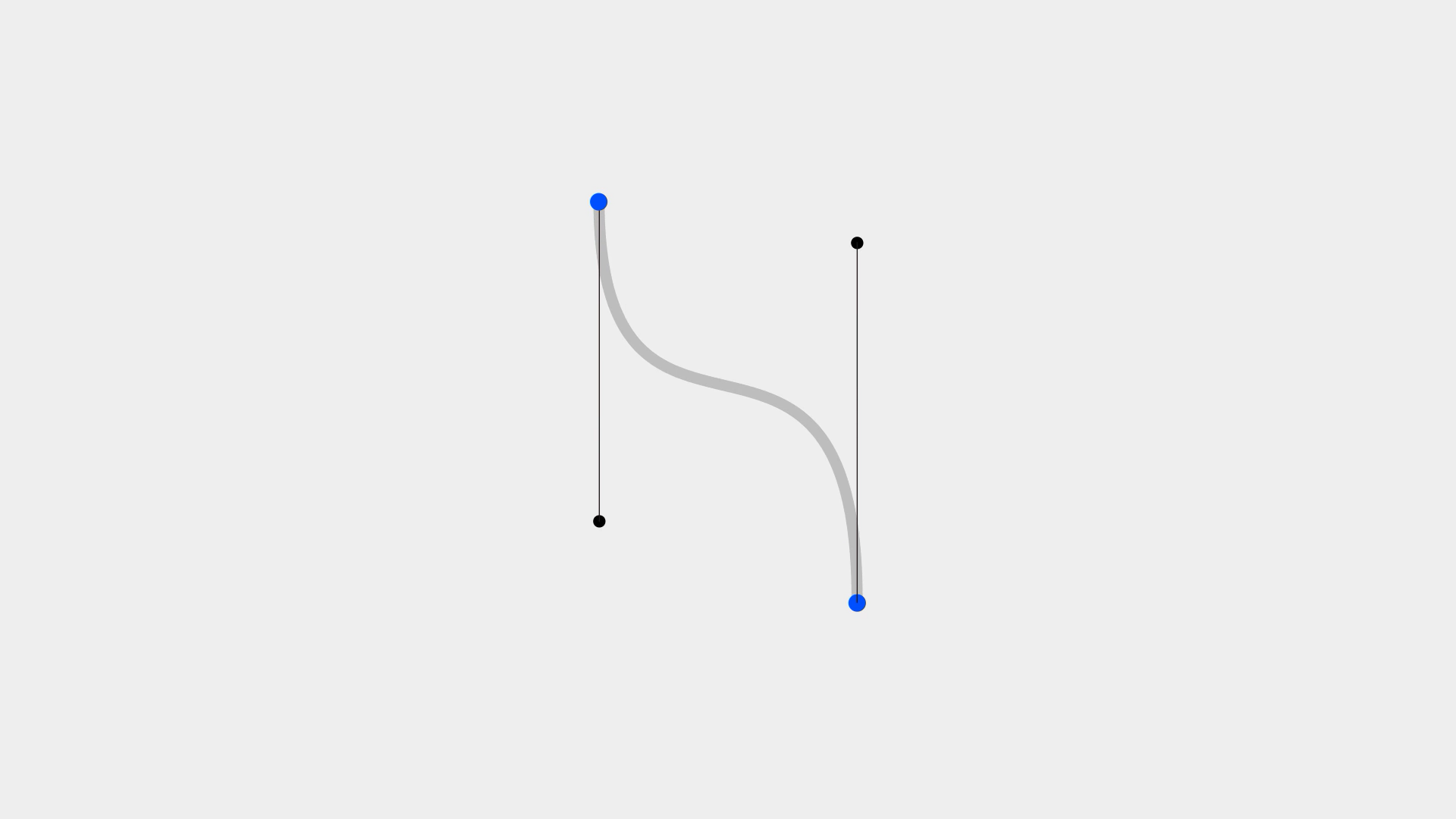
但其實我們將這個節點刪除，拉長兩端的手柄，同樣可以繪制出這個形狀。如此看來，之前中間的點就是在徒增煩惱。這個案例告訴我們，要在滿足效果的前提下，盡可能簡化節點的數量。即便如此，一個圖形還是有可能以多種不同的布點方式繪制出來，都是熟能生巧和經驗之談了，需要我們勤加練習。

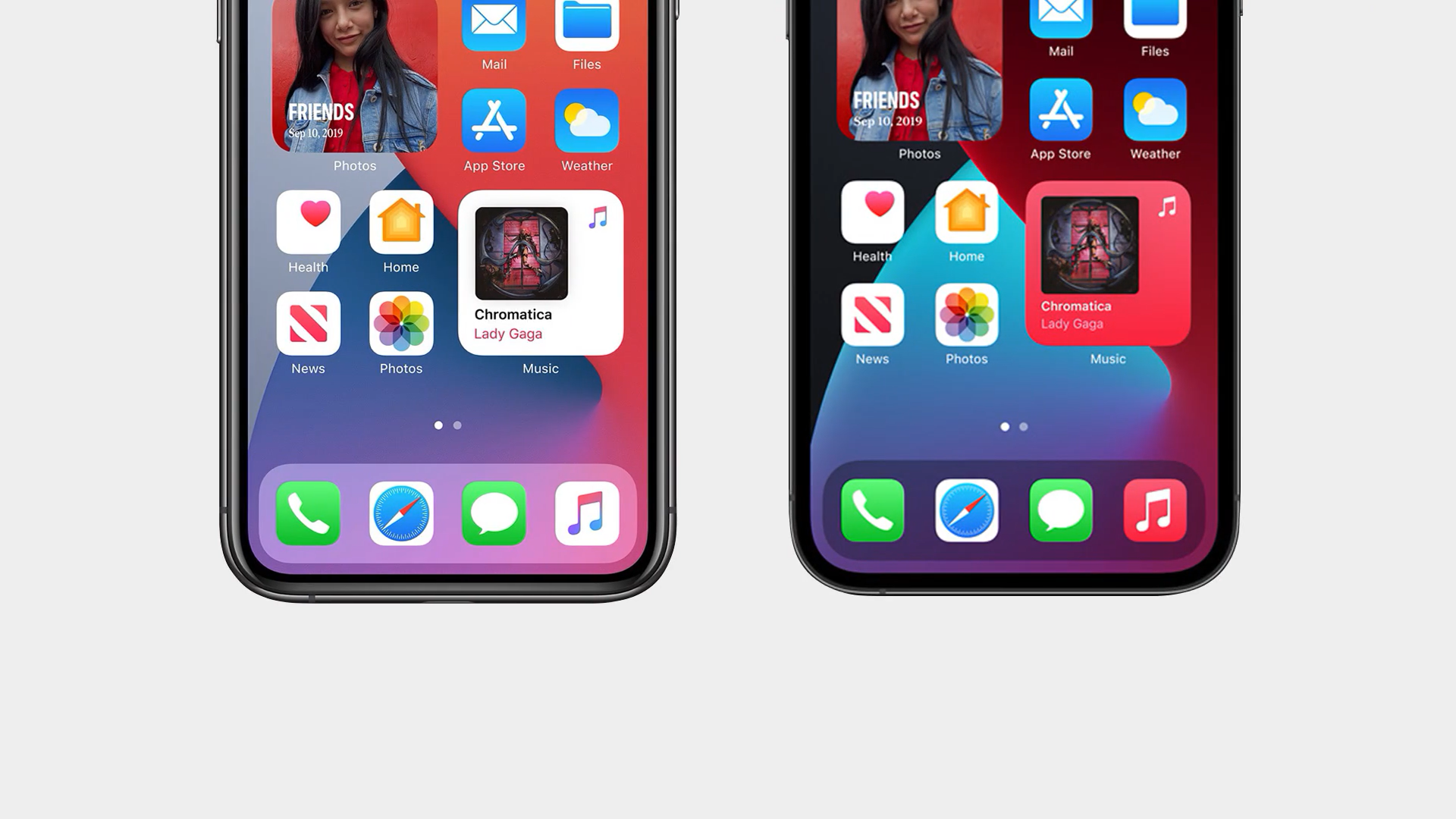
這是 X 底部的 Dock 欄，而這是 12 底部的 Dock 欄。相同的系統，卻有著完全不同曲率的圓角。這是為了和機身外觀的圓角形成更好的呼應。曲率從工業設計走進圖形領域，從平面之外傳播到平面之內，這一條條排比舒適的順滑曲線卻又讓它在平面之內超越了平面。

我們在設計的究竟是什么，是圓角嗎？不。

是在設計一個更接近完美的答案。